What is Simple Linear Regression?

몇가지 통계량의 정의

Simple linear regression의 설명에 앞서, 데이터 (x_1, x_2, ..., x_n), (y_1, y_2, ..., y_n)이 주어졌을 때, 몇가지 통계량(statistics, 주어진 데이터로 부터 계산되어지는 값)을 아래와 같이 "정의"하여 보자.

 

 

Model

Simple linear regression의 모델은 다음과 같다.

 

 

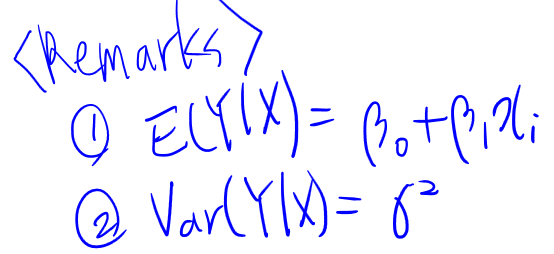
초심자가 단순선형회귀분석을 이해하는 데에 있어 가장 중요한 것은 어쩌면 알 수 없는 것이 무엇인지 아는 것일지도 모르겠다.

 

새로운 x_*가 주어졌을 때, 아직 일어나지 않은 y_*가 무엇인지 알고 싶은 사람은 베타0, 베타1, 그리고 e_*값이 필요하다. 베타0, 베타1을 모르는 것은 그렇다 쳐도 e_*는 확률분포를 따르는 random한 양으로 더 상황이 좋지 않다. 시그마제곱을 안다고 해도 e_*를 정확히 알기는 힘들 것 같으니, 아무래도 y_*를 정확히 알 수는 없을 것 같다. y_*를 정확히 아는 것은 베타0, 베타1, 시그마제곱을 자기만 알고있는 도사님이 있다고 해도 꽤 난제인 것이다 (도사님들도 운빨이 좋아야 맞출 수 있다).

 

불행히도, 베타0, 베타1, 시그마제곱, 그리고 e_1, e_2, ..., e_n은 우리가 관측할 수 있는 양이 아니다. 그러니 그 값이 무엇인지 묻지 마시라 (물어봤자 도사님 빼고는 알려줄 수 있는 사람은 없다).

 

베타0, 베타1, 시그마제곱은 관측불가능한(unobservable) 양으로써 우리가 알 수 없는 값이다. error(e_1~n) 역시 베타0, 베타1을 관측할 수 없기 때문에 우리가 관측할 수 있는 양이 아니다.

 

여기서 우리는 최초에 목표하였던 도사님도 모르는 y_*를 추정하는 데 필요한, 베타0, 베타1, 그리고 시그마제곱(e_*와 관련된 양)을 추정하는 것을 목표로 하자.

  - 보통 추정값에는 추정하고자 하는 양과 동일한 양이 아님을 표시하기 위해 햇(hat, ^) 표시를 한다.

 

OLS estimator

흔히 ordinary least squares estimation이라는 방법을 이용하여 추정한다 (우리가 정해놓은 좋은 추정 방법이다. 마음에 들지 않는다면 다른 방법을 사용해도 좋다). OLS estimation은 아래와 같은 loss function (또는 cost function)을 최소화하는 베타0와 베타1을 베타0와 베타1의 추정값으로 정하는 방법이다.

 

 

이제 베타0, 베타1, 시그마제곱의 추정값을 얻었으니, y_*값을 예측해서 맞추는 행운이 당신에게 올지도 모르겠다.